Chemistry: The pH Scale
The pH Scale
As you might imagine, it's useful to be able to measure the acidity of solutions. For example, the shaving cream I use in the morning has an acid listed on the ingredient label. Clearly, I would have a less enjoyable shaving experience if my shaving cream were as acidic as battery acid!
Scientists have come up with the pH scale for determining the concentration of acid in a solution so we can distinguish between solutions with varying acidity. The pH of a solution can be determined using the following equation:
- pH = -log[H+]
where [H+] is the concentration of H+ ions, in mol/L. The value of pH itself is unitless, so you can get away with saying that "the pH of this solution is 4.54" without any trouble.
Solutions with a pH less than seven are acidic. Solutions with a pH greater than seven are basic. If a solution has a pH exactly equal to seven, it is neutral.
Molecular Meanings
Though a solution with a pH of 7.001 is basic from a chemical standpoint, it's very common for people to refer to compounds with a pH near seven as being neutral. Keep in mind that many of the things you would normally consider neutral are either very weak acids or bases.
The following figure shows the acidity of some common substances you may be familiar with:
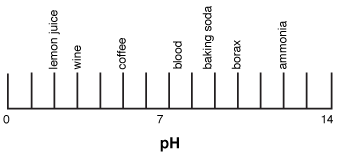
Figure 23.3The pH scale.
It's possible to discover the pH of a solution by using compounds known as "indicators." Indicators are compounds that change colors as the pH of the solution changes. Probably the two most commonly used indicators are litmus (red in acid and blue in base) and phenolphthalein (pronounced "fee-no-thay-leen," colorless in acid, pink in base).
Finding the pH of a Strong Acid
Strong acids are acids that very nearly completely dissociate when you put them into water. That is, almost every molecule of the acid HA that's placed into water breaks up completely to form H+ and A- ions. Some common strong acids include HCl, HBr, HI, HNO3, and HClO4.
Molecular Meanings
Strong acids almost completely break apart in water (a process called dissociation) to make H+ and A- ions.
Because strong acids completely dissociate in water, the concentration of H+ in solution is the same as the concentration of the acid you started with. For example, the pH of a 0.00500 M HCl solution would be:
- -log(0.00500 M) = 2.30
You've Got Problems
Problem 1: What is the pH of a solution with a volume of 475 mL containing a total of 1.20 grams of hydrochloric acid?
Finding the pH of a Weak Acid
Weak acids are acids that stay mostly undissociated in water. As a result, their dissociation is an equilibrium with the following general form:
- HA ⇔ H+ + A-
The equilibrium constant for this expression is given the symbol Ka, which stands for acid-dissociation constant. Some common weak acids include acetic acid and formic acid.
Molecular Meanings
Weak acids are acids that only dissociate to a small degree in water.
As a result, when we place weak acids in water, the H+ concentration is not the same as the original concentration of the acid. Fortunately, we can use our knowledge of aqueous equilibria (Solution Chemistry/emical Equilibria) to find the acid concentration.
Example: What's the pH of a 0.500 M acetic acid solution? Ka (C2H3O2H) = 1.75 × 10-5.
Solution: The equilibrium formed when acetic acid dissociates in water is expressed by the following equation:
- C2H3O2H ⇔ C2H3O2- + H+
To determine the concentration of both, we need to set up the expression for the equilibrium constant (go back to Solution Chemistry/emical Equilibria if this doesn't make sense):
- [C2H3O2-][H+]⁄[C2H3O2H]
Initially, the concentration of acetic acid is 0.500 M. However, at equilibrium, some of the acetic acid will have dissociated, so the concentration of the acetic acid will have decreased. Since we don't yet know how much acetic acid will have dissociated, we'll express this quantity as "x." As a result, the equilibrium concentration of acetic acid is "0.500 - x" M.
For every molecule of acetic acid that dissociates, one acetate ion and one hydronium ion will be formed. Subsequently, the quantity of each ion formed will be equal to "x." Replacing the quantities in the expression above, we get:
- 1.75 × 10-5 = [x][x]⁄[0.500 - x]
- x = 0.00296 M
Because acetic acid is a weak acid with a low equilibrium constant, we'll assume that "x" is a small value compared to 0.500 M. We can then simplify the equation above as:
The Mole Says
Another term that's frequently used to describe the strength of an acid is "pKa," defined as: pKa = -log(Ka)
The concentration of H+ and C2H3O2- ions is 0.00296 M. To find the pH, we'll place this value for [H+] into the equation for pH to get:
You've Got Problems
Problem 2: What's the pH of a 0.750 M formic acid (HCO2H) solution? Ka (HCO2H) = 1.77 × 10-4 M.
- pH = -log[H+]
- pH = -log(0.00296)
- pH = 2.53
Finding the pH of Basic Solutions
What's the pH of a 0.0500 M NaOH solution? This is kind of a funny question because when NaOH breaks up in water, it doesn't form H+ ions. Instead, it forms Na+ and OH- ions, which makes it a basic solution.
This poses a problem. After all, the equation for finding pH requires that you have the concentration of H+ ions, and, as far as we can tell, there are no H+ ions in a basic solution!
Hey, not so fast there, buddy. As it turns out, there are a very small number of H+ ions in basic solutions. These H+ ions are formed when water dissociates in the following way:
You've Got Problems
In pure water, there is a very small quantity of H+ and OH- present from the dissociation of water (10-7 M, to be exact). However, the quantity of each is so small that you can't detect it simply by drinking it.
- H2O ↔ H+ + OH-
As a result, whenever water is present (as it must be in an aqueous solution), there will be a few H+ and OH- ions—not many, but a few. The equilibrium constant for the dissociation of water has the symbol "Kw". Kw is equal to 10-14.
This turns out to be handy for those of us wanting to find the pH of a basic solution. The reason for this is that the previous equation yields the following equilibrium expression:
- Kw = [H+][OH-]
So if we know the concentration of base, we can use this expression to find the concentration of acid.
Example: What is the pH of a 0.0500 M NaOH solution?
Solution: Using the equilibrium expression for water and replacing the values with what we know, we get:
You've Got Problems
Problem 3: What's the pH of a 0.00340 M LiOH solution?
- Kw = [H+][OH-]
- 1.00 × 10-14 = [H+][0.0500]
- [H+] = 2.00 × 10-13 M
To find pH, we simply use the equation:
- pH = -log[H+]
- pH = -log[2.00 × 10-13]
- pH = 12.7
This answer indicates a very basic solution, which is what we would expect from a 0.0500 M NaOH solution.

Excerpted from The Complete Idiot's Guide to Chemistry © 2003 by Ian Guch. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.
To order this book direct from the publisher, visit the Penguin USA website or call 1-800-253-6476. You can also purchase this book at Amazon.com and Barnes & Noble.
