Algebra: Investigating Variation
Investigating Variation
There is an undeniable cause-and-effect link between many things in life. You may intuitively feel these connections every once in a while and accept their universal truths without even noticing it. In some cases, an increase in one event causes an increase in another; for example, the more french fries you eat at a fast food restaurant, the bigger your waist will expand. The faster you drive, the more likely you are to get a speeding ticket.
On the other hand, there are also events that are paired up in the opposite (or inverse) way: An increase in one leads to a decrease in the other. I was once told that the number of keys you carry around with you at the office is inversely related to how successful you are at work. (In other words, the big boss only has one or two keys, because they open everything, but the worker bees have key rings that might as well belong to a zookeeper.) For those of you calloused to the world of government, how about this inverse relationship: The more successful you are at politics, the less honest you probably are as a person. (Ooh, a cheap shot!)
These relationships are called variation, and in this section, you'll learn to express them mathematically using rational equations.
Direct Variation
Direct variation is the relationship I described in which an increase in one value corresponds with an increase in the other, like in the statement "The longer you study for a test, the higher your score will be." In this case, an increase in study hours should correlate with an increase in the percentage test score.
Talk the Talk
If the variables x and y exhibit direct variation, then y is exactly k times as large as x; k is called the constant of proportionality. Direct variation is also called proportional variation.
In algebra, however, you'll only look at a very specific kind of direct variation: When one value is multiplied by a number k (called the constant of proportionality), then the corresponding value will increase by exactly k times as well. Mathematically speaking, if x and y are directly related, then
- y = k · x
meaning that y is exactly k times as big as x. For example, if my test score directly (or proportionally) varies with the number of hours I spent studying, then studying twice as long must double my test score. Furthermore, the test score I get after studying for three hours must be exactly three times as large as the test score I would have gotten had I studied for only one hour.
Usually, your first job in a direct variation problem is calculating that constant of proportionality, and you do that by dividing the two numbers which are directly related. So, if y varies directly with x, then
Once you find k, you can use that equation to find any missing value.
Example 3: Assume that the measurements of the Statue of Liberty's facial features vary directly with the measurements of my facial features. The length of the statue's nose measures 54 inches, and the length of my nose measures 2.375 inches, as illustrated in Figure 18.2. If Liberty's right eye measures 30 inches across, calculate the distance across my right eye. (Round all calculations to the thousandths place.)

Figure 18.2The Statue of Liberty may have a large nose, but my nose is no small matter either, and I have no pointy hat to draw attention away from it.
Solution: Since direct variation is exhibited, divide the statue's nose measurement by mine to determine the constant of proportionality. I suggest using a calculator unless you're really excited about long dividing by hand.
Now that you know the value of k, it's time to calculate eye width. You should use the equation
Where do you plug in her eye measurement, for y or for x? It depends upon where you put her measurement when you calculated k. Notice that the 54-inch honker appeared in the numerator, so her enormous measurement must once again appear in the numerator of this equation.
You can rewrite this equation as a proportion, if you express 22.737 as the equivalent fraction 22.7371 and solve via cross multiplication.
- 30.1 = x(22.737)
My eye is approximately 1.32 inches across. Of course, it would have just been easier to measure my eye than do all that math, but then again, you couldn't have measured my eye, because you don't have ready access to it. I'm not about to start loaning it to people just so they can get answers quicker. How could I be sure you'd mail it back to me?
You've Got Problems
Problem 3: The variables x and y vary proportionally, and when x = 12, y = 15. Determine the value of y when x = 35.
Indirect Variation
Indirect (or inverse) variation occurs when an increase in one quantity leads to a decrease in the other. Specifically, when one quantity increases to n times its original amount, the other will decrease to 1n times its original amount.
Talk the Talk
If two quantities, x and y, exhibit indirect (or inverse) variation, then their product remains constant even as the values of x and y change: xy = k. This means that as one quantity becomes n times as large, the other must become 1n times as big.
Because of this, the product of the indirectly related quantities will always be a constant:
- xy = k
How is this possible? Watch what happens if x in this equation becomes n times as large and y becomes 1n times as big:
Critical Point
In The Simpsons episode "HOMR," the reason for Homer's lack of intellectual acuity is revealed (in other words, we find out why he's such a dummy): There's a crayon stuck in his brain that's been lodged there since childhood. Doctors remove it, and suddenly, he becomes a brainiac. However, it turns out to be a mixed blessing, because people shun the new, smarter Homer.
Grieved, he goes to talk to his superintelligent daughter, Lisa, who affirms that his worst fears have been realized. "Dad, as intelligence goes up, happiness often goes down. In fact, I made a graph," she says, and holds up Figure 18.3. "I make a lot of graphs," she sighs sadly.
This is the graph of an inverse variation. Notice that as x gets bigger and hence you get smarter, y gets smaller (the graph gets lower and lower the further right you go), meaning your happiness is decreasing.
Inversely, the smaller your intelligence (the closer to the origin you are along the x-axis), the higher the graph stretches, meaning a happier person.
Who says you couldn't learn something from watching television? In fact, The Simpsons series features tons of mathematical jokes and references. Check out Dr. Sarah J. Greenwald and Dr. Andrew Nestler's website at www.simpsonsmath.com.
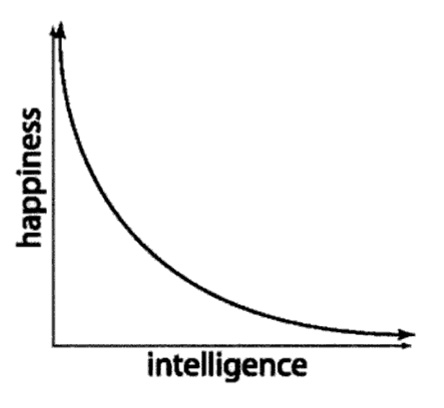
Figure 18.3Lisa has bad news for her newly intelligent father.
Direct and inverse variation are actually very closely related. Remember, in direct variation, it was the quotient of the two values that remained constant (yx = k), whereas inverse variation features a constant product (xy = k). Once again, your first job in an inverse variation problem will be to calculate that constant and then use it in the equation xy = k to calculate missing values.
Example 4: Suppose that the number of times Oscar brushes his teeth in a year varies inversely with the total number of cavities he'll get that year. In 2003, he brushed his teeth a total of 48 times and got four cavities. If he plans to brush his teeth 140 times this year, how many cavities should he expect? (Round your answer to the nearest whole number.)
Solution: Let t equal the total number of times Oscar brushes his teeth in a year and c equal his total number of cavities for that year. Since the problem tells you that t and c vary inversely, you know that their product will be a constant, k:
- t · c = k
In the year 2003, t = 48 and c = 4, so plug those into the equation to find k:
- 48 · 4 = k
- 192 = k
This year, t will equal 140, and you have to calculate the corresponding c, knowing that k will still equal 192.
- t · c = k
- 140 · c = 192
To solve for c, just divide both sides by 140.
- c = 192140
- c 1.371
The directions indicate that you should round your answer to the nearest whole number, so Oscar should expect one cavity this year, because c = 1 approximately.
You've Got Problems
Problem 4: Assume x varies inversely with y, and that x = 9 when y = 75. Find the value of x when y = 2.

Excerpted from The Complete Idiot's Guide to Algebra © 2004 by W. Michael Kelley. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.
You can purchase this book at Amazon.com and Barnes & Noble.
