Algebra: Maintaining a Balance
Maintaining a Balance
In case you haven't seen one, here's a basic equation:
- 3x - 2 = 19
It looks a lot like an expression, except it contains an equal sign. Just like expressions, equations translate easily into words. The above equation means "2 less than 3 times some number is equal to 19." Your job will be to figure out exactly what that number is. In this case, x = 7, and you can probably figure that out by plugging in a bunch of different things for x until something works. However, guessing is never a great way to reach a solution, so I'll show you a better way.
Think of an equation as a playground seesaw. The left and right sides of the equation sit on opposite sides of the seesaw, and because they are equal, it is exactly balanced, like in Figure 4.1.
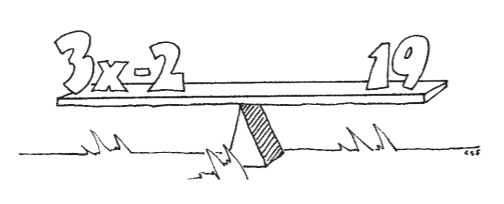
Figure 4.1Since the two sides of the equation are equal, it's as though their weights precisely balance them on a seesaw.
Talk the Talk
The process of forcibly isolating a variable on one side of the equal sign (usually the left side) is called solving for that variable.
Your job when solving equations will be to shift around the contents of the seesaw so that only x remains in the left seat. This process is called solving for x, and it forces the answer to appear, as if by magic, in the right seat. You just have to be careful to keep that delicate balance the whole time.
Adding and Subtracting
Take a look at the equation x - 5 = 11. It's basically asking "What number, if you subtract 5, gives you 11?" You can probably arrive at the answer using only common sense, but let me show you the official mathematical way to get there.
Remember, your final goal is to get x all by itself on the left side of the equation, and the only thing in the way is -5. I want to get rid of that -5, but how? Well, if I add the opposite of -5, that will effectively cancel it out (remember the additive inverse property?). However, if I suddenly add 5 to the left side of the equation, the seesaw will no longer be balanced, and someone's going to come crashing to the ground, possibly with a nasty-looking nosebleed.
To keep the seesaw balanced, I'll have to add 5 to the right side of the seesaw as well:
| x | - | 5 | = | 11 |
| + | 5 | + | 5 | |
| x | = | 16 | ||
Since the sum of -5 and 5 is 0, you get x + 0 (which equals x) on the left side of the equation. Because only x remains on the left side of the equation, the answer appears on the right side, 16.
To see if you're right, go back to the original equation, and replace x with 16:
How'd You Do That?
By replacing x with 16 to check your answer, you're applying the substitution property (another property to add to your list), which allows you to substitute values for one another, as long as they are equal.
- x - 5 = 11
- (16) - 5 = 11
- 11 = 11
Since you get a true statement (11 definitely equals 11), your answer x = 16 was correct.
You've Got Problems
Problem 1: Solve the equation for x.
8 + x = 19
Multiplying and Dividing
In your endeavors to isolate x's to solve equations, you'll often have to eliminate not only numbers added to or subtracted from x, but numbers actually attached to the x, like in the equation 5x = 45. To be precise, the 5 and x are not actually glued to one another. They are actually just multiplied, and 5 is called the coefficient. Therefore the equation is actually asking "5 times what number is equal to 45?"
Talk the Talk
When a number is written next to a variable, that number is called a coefficient. Thus, in the expression 2x, 2 is the coefficient. Note that coefficients are usually written at the front of the expression, before the variable.
To answer that question, you can't add or subtract 5 like in the previous example, because neither addition nor subtraction can cancel out multiplication. You've got two options when it comes to eliminating coefficients; notice that both of the techniques require the same thing be done to both sides of the equation, just like beforeyou've got to keep that seesaw balanced!
- Integer coefficients: If the x has a coefficient of n, divide both sides by n to get your final answer.
- Fractional coefficients: If the x has a rational coefficient ab, multiply both sides of the equation by ba to solve for x. This may look familiar, because it's based on the multiplicative inverse property.
Both of these techniques change the coefficient of x into some fraction cc; in other words, x's coefficient will now have the same number in both the numerator and denominator, and any such fraction is equal to 1. (Remember, any nonzero number divided by itself equals 1.) Therefore, the left side of the equation can be rewritten as 1x, which means the exact same thing as plain old x, so your isolation procedure is complete.
Talk the Talk
Problem 2: Solve the equation.
-45w = 16
Example 1: Solve the equations and check your answers.
- (a) 5x = 45
- Solution: Since the coefficient is an integer, divide both sides of the equation by it.
- 5x5 = 455
- x= 9
- To check the answer of 9, plug it in for x in the original equation.
- 5(9) = 45
- 45 = 45
- (b) 23y = 12
- Solution: Since the coefficient is rational, multiply both sides of the equation by its reciprocal, 32.
- 32 · 23y = 32 · 121
- 66y = 362
- y = 18
- To check the answer, substitute 18 for y in the original equation.
- 23 (181) = 12
- 363 = 12
- 12 = 12

Excerpted from The Complete Idiot's Guide to Algebra © 2004 by W. Michael Kelley. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.
You can purchase this book at Amazon.com and Barnes & Noble.
