Geometry: From One Theorem Comes Many
From One Theorem Comes Many
You haven't had a proof in awhile. “Never let a section go by without a proof,” I always say. Here's an interesting tidbit about inscribed angles that might surprise you.
- Theorem 17.2: The measure of an inscribed angle of a circle is one-half the measure of its intercepted arc.
There are three ways to create an inscribed angle: either one of the sides of the angle is a diameter, each side of the angle lies on different sides of a diameter, or both sides of the angle lie on the same side of a diameter. I have illustrated each of these situations in Figure 17.8.
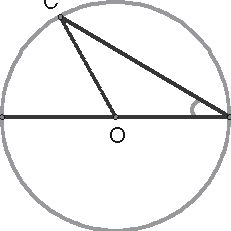
Figure 17.8An inscribed circle where (a) one side of the angle is aBA B diameter, (b) each side of the angle lies on a different side of the diameter ¯ab, and (c) both sides of the angle lie on the same side of the diameter ¯AB.
The proof of the first case requires the most detail. The second and third cases use the first case and the Arc Addition and Angle Addition Postulates.
After you prove this theorem, many other theorems will follow. Their proofs will be very short, because most of the work will have been done here.
- Given: You are given a circle with center O, diameter ¯AB, and inscribed angle ∠ABC. The goal is to prove that m∠ABC is equal to one-half of the degree measure of ˆAC. This situation is shown in Figure 17.8(a).
- Proof: The game plan for this proof involves creating a central angle, because the only way you know to determine the degree measure of an arc is to relate it to the measure of its corresponding central angle. Suppose ∠ABC is inscribed in a circle with center O, as shown in Figure 17.8(a). The goal is to relate that degree measure of ˆCA and m∠CBA. Let's make a triangle.
- You might be tempted to make ΔABC , but then you would have two of the sides being chords, and one side being a diameter. You wouldn't have enough useful information to draw any conclusions. The other triangle you can make is ΔCOB. This triangle is useful for two reasons. The first reason is that you havea central angle, ∠COA, which will enable you to find the degree measure of ˆCA (the arc you want to relate to your angle). The second reason that this triangle is useful is that two of its three sides are radii of the circle. Because all radii of a circle are congruent, you will have created an isosceles triangle. Isosceles triangles have the property that the angles opposite the congruent sides are congruent: ∠OCB ~= ∠OBC. Because ∠COA is an exterior angle to ΔCOB, you know that m∠COA = m∠OCB + m∠OBC. Because you know the degree measure of ¯CA is equal to m∠COA, the desired relationship will be established. Let's organize this proof into its columns.
| Statements | Reasons | |
|---|---|---|
| 1. | A circle with center O, diameter ¯AB, and inscribed angle ∠ABC | Given |
| 2. | Construct the radius ¯CO | Postulate 3.2 |
| 3. | ¯CO ~= ¯OB | Theorem 17.1 |
| 4. | ΔCOB is an isosceles triangle | Definition of isosceles triangle |
| 5. | ∠OCB ~= ∠OBC | Theorem 12.1 |
| 6. | m∠OCB = m∠OBC | Definition of ~= |
| 7. | ∠COA is an exterior angle to ΔCOB | Definition of exterior angle |
| 8. | m∠COA = m∠OCB + m∠OBC | Theorem 11.3 |
| 9. | m∠COA = 2m∠OBC | Substitution (steps 6 and 8) |
| 10. | m∠OBC = 1/2m∠COA | Algebra |
| 11. | ∠COA is a central angle | Definition of central angle |
| 12. | The degree measure of ˆAC is equal to m∠COA | Central Angle Postulate |
| 13. | m∠OBC is equal to one-half the degree measure of ˆAC | Substitution (steps 10 and 12) |
Now that the proof of Theorem 17.2 is out of the way, you can prove several other theorems and calculate some arc and angle measures.
- Theorem 17.3: An angle inscribed in a semicircle is a right angle.
This situation is illustrated in Figure 17.9. Because an inscribed angle has a measure equal to one-half the measure of the intercepted arc, and a semicircle has degree measure equal to 180º, you know that the inscribed angle has measure equal to one-half of 180º, which happens to equal 90º, which means that the inscribed angle is a right angle. Nothing too earth-shattering there!

Figure 17.9An angle inscribed in a semicircle.
- Theorem 17.4: If two inscribed angles intercept the same arc, then these angles are congruent.
Again, each inscribed angle has measure equal to one-half of the measure of the intercepted arc. Look at Figure 17.10. Because the same arc is intercepted, each inscribed angle has the same measure, so the two inscribed angles are congruent. These theorems seem to fall out naturally from Theorem 17.2!

Figure 17.10Two inscribed angles, ∠CBD and ∠CAD, intercept the same arc.
- Example 4: If, in Figure 17.11, m∠CBD = 34º , find the degree measure of the minor arc ˆCD.
- Solution: Because the measure of the inscribed angle is one-half the degree measure of the intercepted arc (or the degree measure of the intercepted arc is twice the measure of the inscribed angle), the degree measure of ˆCD is twice m∠CBD , or 68º.
Here's your chance to shine. Remember that I am with you in spirit and have provided the answers to these questions in Answer Key.
- 1. Find the circumference of the circle and the length of ˆRST in Figure 17.11.

Figure 17.11The circle with radius length 10 feet, and m∠ROT = 155º.
- 2. Find the area of a circle whose radius has a length of 3 feet.
- 3. Find the area of a sector with a radius of length 6 inches and a central angle measuring 150º.
- 4. If, in Figure 17.10, the degree measure of the minor arc ˆCD is 56º, find m∠CBD.

Excerpted from The Complete Idiot's Guide to Geometry © 2004 by Denise Szecsei, Ph.D.. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.
To order this book direct from the publisher, visit the Penguin USA website or call 1-800-253-6476. You can also purchase this book at Amazon.com and Barnes & Noble.
