Geometry: How Many Midpoints Are There?
How Many Midpoints Are There?
Mathematicians talk about the midpoint of a segment as if it is the only one. It makes sense that there is only one “middle” of a segment, but suppose someone has just challenged you to prove it. Not only will you get practice writing proofs, but you'll get to dust off your algebra skills and put them to work as well.
There are a couple of ways that you can prove that a line segment can only have one midpoint. You can try the direct approach: Start with a line segment, find the midpoint and show that no other point on the segment has what it takes to be a midpoint. This approach is difficult. You would have to examine each point on the segment for its midpoint potential. Unfortunately, there are infinitely many points on a line segment. Even if you dedicated the rest of your life to completing this process, it would not be enough.
In this situation a direct approach is much more difficult than an indirect approach. To use an indirect approach, turn to the negative of your conclusion. The conclusion is that the midpoint is unique, or that there is only one midpoint. The negative of that statement is that the midpoint is not unique. There is not only one. That means that there must be at least two midpoints.
This method of an indirect proof is often referred to as a “proof by contradiction.” You start by assuming that the conclusion is false (in this case, that the midpoint is not unique), and try to contradict one of your definitions, postulates, theorems or assumptions. Let's see how it all plays out.
- Example 2: Prove that the midpoint of a segment is unique.
- Solution: Go through the five steps involved in writing a formal proof.
- 1. Give a statement of the theorem:
- Theorem 9.2: The midpoint of a segment is unique.
- 2. Create a drawing to visualize what's going on. You'll need a line segment; call it ¯AB. You'll also need two midpoints, which you can call M and N. I've drawn everything you'll need in Figure 9.2.
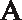
Figure 9.2¯AB has two distinct midpoints M and N
- 3. State what is given in terms of the drawing. You are given a line segment ¯and two distinct midpoints M and N.
- 4. State what you want to prove in terms of the drawing. According to your drawing, the line segment ¯has been broken up into three segments: ¯AM, ¯MN, and ¯NB. You don't have many definitions or theorems about segments that you can contradict, but there is the Ruler Postulate: The measure of any line segment is a unique positive number. If you can somehow show that MN = 0, you will contradict this postulate. So that's what you'll do. Prove: MN = 0.
- 5. Write the proof. Your game plan is to somehow argue that MN = 0. You can only use the fact that both M and N are midpoints, and use Theorem 9.1. It's going to take some algebra, but you can do it. Put down your columns and walk through the argument step-by-step. Remember to start with the given information, and stop when you have shown that MN = 0.
| Statements | Reasons | |
|---|---|---|
| 1. | M and N are both midpoints of ¯AB | Given |
| 2. | AM = 1/2 AB and AN = 1/2 AB | Theorem 9.1 |
| 3. | AM + MN + NB = AB | Segment Addition Postulate |
| 4. | 1/2 AB + MN + 1/2 AB = AB | Substitution (steps 2 and 3) |
| 5. | AB + MN = AB | Algebra |
| 6. | MN = 0 | Subtraction property of equality |

Excerpted from The Complete Idiot's Guide to Geometry © 2004 by Denise Szecsei, Ph.D.. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.
To order this book direct from the publisher, visit the Penguin USA website or call 1-800-253-6476. You can also purchase this book at Amazon.com and Barnes & Noble.
