Algebra: Graphing Linear Inequalities

Graphing Linear Inequalities

Wouldn't it be great if you suddenly discovered that you had a skill you didn't know about? What if one day, while you're out jogging, you found out that by twisting your right leg just a little, you could suddenly speak Portuguese fluently? (Assuming of course that you couldn't speak Portuguese before.) That'd really be something to write home about! (Perhaps even in Portuguese.) Well, you're about to find out that (with just a slight twist of your right leg) you can graph linear inequalities.

The difference between linear inequalities and the inequalities you've dealt with so far in this section is that the linear ones have two variables, usually x and y. The great thing about these linear inequality graphs is that they are based on the graphs of linear equations, which you already know how to create. However, if you compare the graphs of linear equations with the graphs of linear inequalities, these are the major differences you'll see in the inequality graphs:

• The graph is not always a solid line. If the inequality symbol in the statement is either < or >, then the line in the inequality graph will be dotted, not solid, to indicate that the points along the line are not solutions to the inequality. However, if the inequality symbol is ‰¤ or ‰¥, the line will be solid, just like you're used to.
• The solution is not just the line, it's an entire region of the graph. The lines (whether solid or dotted) split the coordinate plane into two parts, sort of the way a fence divides up a piece of property. All of the points on one side of the line will make the inequality true, whereas all the points on the other side will not. You indicate the region of solutions by lightly shading it on your graph.

Therefore, to graph a linear inequality, first treat it as though it were a line, and graph that line. (Make sure to check whether the line should be solid or dotted, based on the inequality symbol.) Then choose a coordinate, called a test point, from the coordinate plane and plug it into the original inequality. If it makes the inequality true, then so will all the other points on the same side of the line you drew, so you should shade in that region. If it doesn't work, then the region on the other side of the line is your solution.

Example 8: Graph the inequality 2x - 3y < 12.

Solution: For just a moment, pretend that the inequality symbol is an equal sign, and graph the resulting linear equation. (Since the inequality does not indicate "or equal to," make the line dotted, as shown in Figure 7.7.) The easiest way to graph the line is to calculate its intercepts using the method of Graphing Linear Equations.

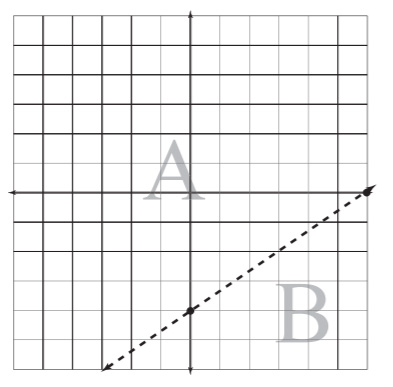
Figure 7.7This is not yet the final graph, but notice how the line splits the coordinate plane into two regions, labeled A and B for clarity.

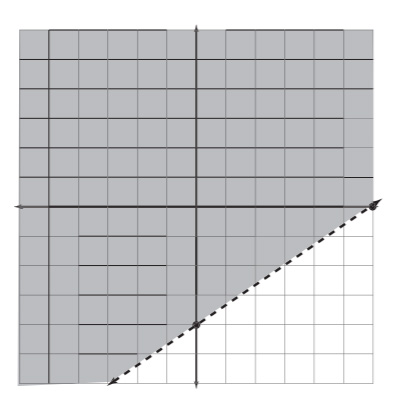
The graph of 2x - 3y < 12 in all its splendor. Looks shady to me €¦.

Now you should choose a test point from one of the two regions. I usually choose the origin, because what could be easier than plugging in 0 for both x and y? Whatever point you choose, plug in its x-coordinate for x in the inequality and its y-coordinate for y. Here's how it works for the origin:

• 2(0) - 3(0) < 12
• (0) < 12

Because this statement is true (0 is, indeed, less than 12), the origin is a solution point, and so is every other point in its region of the plane (region A, in Figure 7.7). So, shade in that portion of the graph to get your final graph (see Figure 7.8).

Excerpted from The Complete Idiot's Guide to Algebra © 2004 by W. Michael Kelley. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.

To order this book direct from the publisher, visit the Penguin USA website or call 1-800-253-6476. You can also purchase this book at Amazon.com and Barnes & Noble.