Geometry: Proofs About Alternate Angles
Proofs About Alternate Angles
You can use Postulate 10.1 to prove lots of theorems. Most of these theorems will travel in pairs. Here are the first of many pairs of theorems.
- Theorem 10.2: If two parallel lines are cut by a transversal, then the alternate interior angles are congruent.
- Theorem 10.3: If two parallel lines are cut by a transversal, then the alternate exterior angles are congruent.
I'Il write out a proof of Theorem 10.2 and give you the opportunity to prove Theorem 10.3 at the end of this section. To prove Theorem 10.2, you'll need a couple of parallel lines cut by a transversal, two alternate interior angles, and an angle that corresponds to one of those alternate interior angles. Figure 10.5 shows the important angles.
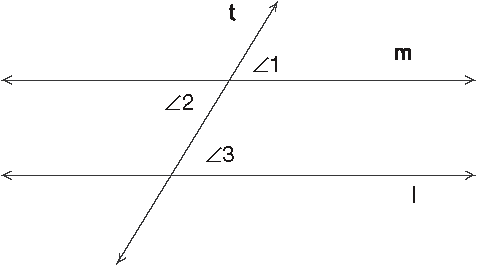
Figure 10.5l m cut by a transversal t.
- Given: l m cut by a transversal t.
- Prove: ∠2 ~= ∠3
- Proof: The game plan is straightforward. ∠1 and ∠3 are corresponding angles, so they are congruent by Postulate 10.1. ∠1 and ∠2 are vertical angles, so you know that they are congruent. The transitive property of ~= provides the rest.
| Statements | Reasons | |
|---|---|---|
| 1. | 1 m cut by a transversal t | Given |
| 2. | ∠2 and ∠3 are alternate interior angles | Definition of alternate interior angles |
| 3. | ∠1 and ∠3 are corresponding angles. | Definition of corresponding angles |
| 4. | ∠1 and ∠2 are vertical angles | Definition of vertical angles |
| 5. | ∠1 ~= ∠3 | Postulate 10.1 |
| 6. | ∠4 ~= ∠8 | Theorem 8.1 |
| 7. | ∠2 ~= ∠3 | Transitive property of ~= |

Excerpted from The Complete Idiot's Guide to Geometry © 2004 by Denise Szecsei, Ph.D.. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.
To order this book direct from the publisher, visit the Penguin USA website or call 1-800-253-6476. You can also purchase this book at Amazon.com and Barnes & Noble.
