Chemistry: Valence Shell Electron Pair Repulsion Theory (VSEPR)
Valence Shell Electron Pair Repulsion Theory (VSEPR)
Take a look at the heading for this section. Valence Shell Electron Pair Repulsion Theory (VSEPR). Say it five times quickly. No matter how you look at this phrase, it doesn't sound like something fun.
However, I've got great news for you. The VSEPR (pronounced "vesper") theory is something we've already discussed. VSEPR theory simply states that the pairs of electrons in a chemical compound repel each other and move as far from each other as possible because they have the same charge.
Molecular Meanings
Valence Shell Electron Pair Repulsion Theory (VSEPR) states that the shapes of covalent mole cules depend on the fact that pairs of valence electrons repel each other.
See, I told you it wasn't that hard. We already knew electrons repel each other—heck, we already talked about it a little bit earlier in this section. The big question, of course, is "how will this theory affect us personally?" Good question.
What Does VSEPR Have to Do with Hybrid Orbitals?
When we discussed hybrid orbitals, we mentioned the bond angles associated with each type of orbital. These bond angles represent the greatest possible angles between neighboring pairs of electrons. For example, if we look at a picture of the three sp2 orbitals in an atom, we can see that they stretch as far away as possible, 120º:
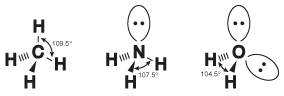
Figure 10.11The farthest that the electrons in the three bonds can be distanced from each other in space is 120º. The shape associated with this bond angle is "trigonal planar."
As it turns out, there's a little more to knowing bond angles than just knowing the hybridization of the central atom in a molecule. While the pairs of electrons in a covalent bond are situated mainly between the two bonding atoms, the electrons in a lone pair spread out a little bit. Because these lone pairs spread out their negative charge, the chemical bonds are repelled a bit more by lone pairs than by each other. Therefore, the bonds in covalent compounds with lone pairs tend to be squished together and have smaller bond angles than predicted solely by the hybridization. This phenomenon is shown in the following figure:

Figure 10.12Though all three of these molecules exhibit sp3 hybridization around the central atom, the bond angles get successively smaller because of the increasing numbers of lone pairs.
Bond Angles and Molecular Shapes the Easy Way

Figure 10.13 Once you have a valid Lewis structure, you can use this flow chart to find the hybridization, bond angle, and shape of any atom on any covalent compound!

Figure 10.14The Lewis structure of phosphorus tribromide.
So how can ordinary people like you or me remember the bond angles and shapes of all the atoms in all the covalent compounds known to man? We could memorize them, but that would be really boring and cut into our valuable television time. Instead, we'll use the Lewis structures we learned earlier to give us a hint about how covalent molecules are put together.
You've Got Problems
Problem 3: Find the hybridizations, shapes, and expected bond angles of the central atoms in the following molecules:
(a) SiO2
(b) CH2O
(c) OF2
Here's how you use this flow chart.
- At the top, you're asked, "How many atoms are bonded to the atom of interest?" In our case, the atom of interest is whatever atom you're trying to find the hybridization and shape of. For PBr3 (see the following figure), the answer would be "3." Follow the arrow labeled "3" to the next question.
- The second question asks, "How many lone pairs does the atom of interest have?" In our case, phosphorus has one lone pair. As a result, we follow the arrow marked "1" to find that phosphorus tribromide is trigonal pyramidal, has a bond angle of 107.5º, and is sp3 hybridized.
This flow chart can be used to find the hybridization, bond angle, and shape of any covalently bonded atom. The next time you're at a dinner party, you can use this information to wow the guests with your immense knowledge of hybridization and VSEPR theory.

Excerpted from The Complete Idiot's Guide to Chemistry © 2003 by Ian Guch. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.
To order this book direct from the publisher, visit the Penguin USA website or call 1-800-253-6476. You can also purchase this book at Amazon.com and Barnes & Noble.
