Algebra: It's a Slippery Slope
It's a Slippery Slope
The slope of a line is a number that describes how "slanty" that line is. Is the line steep or shallow? Does it rise from left to right or fall? Even if you don't have the graph of the equation, you can answer all of these questions knowing only the slope of the line in question.
Calculating Slope of a Line
As useful as the slope of a line is, it's remarkably easy to calculate. All you have to do is pick out two points on the line, which I'll call points A and B, for reference. The slope of the line is equal to this fraction:
- number of vertical units it takes to get from A to Bnumber of horizontal units it takes to get from A to B
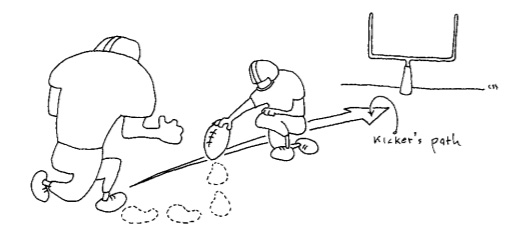
Figure 5.7To position himself correctly, the kicker takes two steps back from the ball and then two steps left.
Talk the Talk
You can also calculate the slope of the kicker's approach by going from the kicker to the ball, rather than vice versa. In that case, the numerator is 2 (two steps forward or up) and so is the denominator (two steps right). So, the slope equals 22, which simplifies to 1. So, no matter which you consider the starting and ending point, you get the same answer.
Let me explain what I mean in terms of a real-life exampleplacekicking in football. Whenever a kicker comes onto the field to try for an extra point or a field goal, he must make sure that his path to the ball is precise. He needs to get a running start at the ball to give his kick some momentum. (If he just stood there and swung his leg, the ball wouldn't go very far.) However, if his running path is off course, the ball won't go exactly where he's intending it.
To make sure their approach paths are exactly right, all right-footed kickers do the same thing: They stand over the ball, take two steps backward, and then two steps to their left to reach their starting position. This creates an imaginary line of approach, which passes through two points: The position of the ball and their starting position, as shown in Figure 5.7.
Talk the Talk
Make sure to subtract the y-values in the numerator and x values in the denominator. Students often reverse them, mistakenly placing the x's in the top of the fraction, so be cautious.
Imagine we're looking down at the field, perhaps from an airplane or a blimp advertising tires, and you can easily calculate the slope of that approach line. The slope's numerator is equal to the number of steps he takes forward or backward (up or down as we look down on the field); since he backs up two steps from the ball, the numerator will be -2. (If he'd have gone forward, and moved up according to our perspective, the number would have been positive.)
You've Got Problems
Problem 4: Calculate the slope of the line passing through the points (4,0) and (-5,6).
The denominator of the slope equals the number of steps he takes left or right, where left steps are negative and right steps are positive. Since he takes two steps left, the denominator equals -2. Therefore, the slope of the line is:
- -2-2 = 1
Talk the Talk
What does it mean when a vertical line has an undefined slope? Basically, the slope of a vertical line is an illegal number. Take, for example, the vertical line x = 3; I'll choose two random points from the line, (3,4) and (3,9), and use the slope formula:
9 - 43 - 350
Did you know that you're not allowed to divide by 0 in math? It's illegal! It's just as much an anathema as ripping those little mattress tags off.
Any fraction with 0 in the denominator (but not in the numerator) is said to be undefined, so that's why your textbook says the slope of a vertical line is undefined, or that the line has "no slope."
How can you remember that vertical slopes are undefined but horizontal slopes are 0? Think about trying to walk along the lines. How much effort would it take to walk along a horizontal line? Zero.
How much effort would it take to walk along a vertical line? You can't! It's impossible, because there is no slope in a vertical line. It'd be like trying to walk up a wall, and unless you have been bitten by a mutant spider, wear brightly colored red-and-blue spandex, and have a girlfriend named Mary Jane, that skill's probably not on your resum©.
So, you can easily calculate the slope of a line by picking two of its points and counting the number of steps (or units) it takes to get from one to the other. However, this is not a very handy technique, especially if the points' coordinates aren't integers.
There is a handy formula you can use to calculate the slope of a line, given the coordinates of two of its points; the formula basically counts the horizontal and vertical changes for you. It works like this: If a line contains points (a,b) and (c,d), then the slope of the line is equal to
- d - bc - a
In other words, subtract the y-values from one another, and divide that by the difference of the x-values.
Example 4: Calculate the slope of the line that passes through the points (4,-1) and (-3,9) and explain what it means.
Solution: Apply the slope formula, which finds the difference of the y's and divides it by the difference of the x's:
- 9 -(-1)-3-(4) = 9 + 1-3-4 = 10-7 = - 107
Remember, if a fraction is negative, you can rewrite the fraction, placing the negative sign in the denominator or the numerator, so -107 = -107 = 10-7.
What do these slopes mean? A slope of -107 means that you can go down 10 units and right 7 units from one point on the line to reach another point on that line, because that's exactly how to travel from (4,-1) to (-3,9). (Graph those coordinate pairs if you don't believe me.)
Alternatively, the slope 10-7 assures you that you can go up 10 units and left 7 units from one point on the line to reach another point, because that's the path from (-3,9) to (4,-1).
Interpreting Slope Values
You can tell a lot about a line just by looking at its slope. Here are a few facts to familiarize yourself with about the gripping, romantic relationship between a line and its slope:
- Lines with positive slopes rise. If a line's slope is greater than 0, its graph will slant upwards from left to right.
- Lines with negative slopes fall. In other words, the coordinates on the line will have smaller and smaller y values as you travel left to right.
- Lines with large slopes are steep. The further a slope's absolute value is from 0, the steeper its graph will be. In fact, a line with slope 2 is significantly steeper than a line with slope 1, so the steepness increases sharply and quickly as the slope values increase. A line with a slope of -5 is also very steep, it's just slanted in a different direction than lines with positive slopes.
- Lines with small slopes rise more gradually. The closer a slope's absolute value is to 0, the more its graph will resemble a horizontal line.
- Horizontal lines have slopes equal to 0. Any two points on a horizontal line will have the same y value, so when you calculate the slope, the numerator will be 0.
- Vertical lines have undefined slopes. Learn more about this in the nearby sidebar.

Excerpted from The Complete Idiot's Guide to Algebra © 2004 by W. Michael Kelley. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.
You can purchase this book at Amazon.com and Barnes & Noble.
